Visualizing language-script relationships

Graph below was obtained by processing language and script tags of about .5 billion web pages. Different character shapes were obtaining using custom VertexShapeFunction


Full image


Notebook

Graph utilities I use

There's a number of graph utilities and tricks I use when working with graphs in Mathematica 8, I've summarized them in notebook graphUsage.nb. You can get this notebook and all required packages here.

Brief overview:

Fixing annoyances
programmatically changing style of existing graph, modifying graphs without forgetting vertex coordinates, using GraphPlot's layout for Graph objects, aligning adjacency matrix with vertex labels in index graphs

Listing graph structures
cliques, independent sets, maximal cliques, maximal independent sets, hamiltonian circuits

Visualizing graphs
Showing all graphs that miss particular properties, visualizing graphs with intensity attached to vertices -- pieGraph and fadedGraph. Showing graph with several types of vertices.

Computing Lovasz Theta function

One application of semi-definite programming is finding largest independent sets, or largest cliques in graph. According to Lovasz "Semidefinite programs and combinatorial optimization", SDP is the only known tractable way to find largest clique/independent set in perfect graphs.

One approach I've seen relies on the Lovasz theta function. Lovasz theta function is an estimate of independence number of the graph, and theta of graph's complement is guaranteed to lie between graphs's clique number and its chromatic number. Clique number and chromatic number are NP-complete, yet Lovasz theta function can be found in polynomial time using SDP. In perfect graphs and their complements, clique number and chromatic number coincide, which means that estimate from Lovasz theta function becomes exact.

I've put a function to compute Lovasz theta function using CVXOPT into package sdp2 below. You need to have CVXOPT and Pythonika installed as described here You could use it as follows

Install["/Users/Yaroslav/mathematica/Pythonika"];
SetDirectory[NotebookDirectory[]];
Needs["Bulatov`sdp2`"];
theta = lovaszTheta@GraphData[{"Paley", 13}];
RootApproximant@theta

This gives $\sqrt{13}$

Package also has a function "minimizeSpectralRadius" which finds matrix of smallest spectral radius subject to element constraints, and "lovaszComplete" which creates a graph by thresholding solution of "minimum spectral radius" formulation of Lovasz theta function (p.26 of Lovasz). Curiously, lovaszComplete reaches fixed point after 1 iteration for all graphs I tried --


Red edges are original graph, blue are positive entries introduced when solving the SDP


SDP2 package

Semidefinite programming in Mathematica using CVXOPT

One can get access to semidefinite programming from Mathematica by using Pythonika to interface with Python's cvxopt package.

For MacOS 10.6 and Mathematica 8 the following should work

• Install 64-bit Python 2.7 distribution from official site
  
• Get latest cvxopt sources and make
  
• Get Pythonika sources from google site
  
• copy mathlink.framework (in /Applications/Mathematica.app/SystemFiles/Links/MathLink/DeveloperKit/CompilerAdditions/) to /Library/Frameworks directory
  
• Fill correct paths in Pythonika Makefile, also add "-lstdc++ -framework CoreFoundation" linker flags
  
• In Pythonika Makefile, rename libML.a into libMLi3.a
  

If your compilation doesn't work, post a follow-up comment here

Then you can use my package Bulatov`sdp1 to get direct access to one common form of SDP -- maximize a linear function of a matrix subject to positive-definiteness and element value constraints.

As an example application, consider MAXCUT -- find partition of the vertices such that number of edges connecting vertices from different partitions is maximized.



Solution above was obtained by solving a binary integer quadratic program, as follows

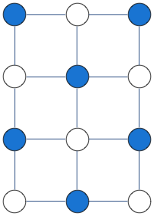
g = GridGraph[{4, 3}];
A = AdjacencyMatrix@g;
n = Length@VertexList@g;
u = ConstantArray[1, n];
vars = x /@ Range@n;
cons = And @@ (-1 <= x[#] <= 1 & /@ Range@n);
solution=vars /. Last[Maximize[{-vars.A.vars, cons}, vars, Integers]]

SDP relaxation gives a guaranteed approximation to binary quadratic program above --

Needs["Bulatov`sdp1`"];
Install["/Users/Yaroslav/mathematica/Pythonika"];
gram = solveDualSDP[-A, IdentityMatrix[n], u];
solution = gramRound[gram];

This gives the same solution for the example above, but is much faster. solveDualSDP here finds psd matrix X that maximizes -A.X with diagonal entries of X constrained to be 1. For more details on this formulation, see Chapter 6 of Williamson,Shmoys, Design of Approximation Algorithms. For details of how to convert SDPs to standard vectorized form as used by CVXOPT, see this post



Packages
Notebook

Plotting over 3d simplex

Someone on stackoverflow asked how to plot a function over 3d simplex.

I put together the code that takes care of rotations into "simplexPlot" and also used a recipe from math.SE for traditional 3D axes. Below is simplex plot of Sin[x y z]




The function "simplexPlot" in notebook plots the function in x-y plane. Function "axes" does traditional 3d axes. To visualize the connection to the original simplex domain, I rotate the whole plot back into original domain

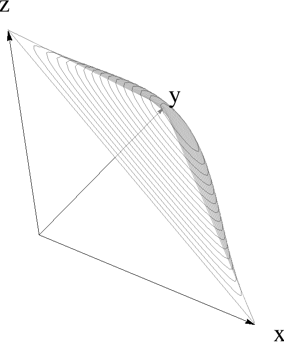
t = AffineTransform[{{{-(1/Sqrt[2]), -(1/Sqrt[6]), 
      1/Sqrt[3]}, {1/Sqrt[2], -(1/Sqrt[6]), 1/Sqrt[3]}, {0, Sqrt[2/3],
       1/Sqrt[3]}}, {1/3, 1/3, 1/3}}];
graphics = simplexPlot[5 Sin[#1 #2 #3] &, Plot3D];
shape = Cases[graphics, _GraphicsComplex];
gr = Graphics3D[{Opacity[.5], GeometricTransformation[shape, t]}, 
   Axes -> False, Boxed -> False, Lighting -> "Neutral"];
Show[gr, axes[1, 1, 1, 0.05, 0.02]]

Notebook

Hyperpublic programming challenge

A start-up put up a small programming challenge.

There was some doubt whether the automatic answer key was correct, so I decided to check the answers using Mathematica. (note, it might be considered cheating to submit solutions obtained using Mathematica)

The first problem asks to find "influence" which comes down to the problem of counting descendants of each node in a graph, and can be done using recursion with memoization. Using Daniel Lichtblau's suggestion on how to parse the adjacency matrix, here's the whole solution.

words = ReadList["challenge2input.txt", Word];
mat = Map[Characters, words] /. {"O" -> 0, "X" -> 1};
inf[i_] := (inf[i] = 
    1 + If[Total[mat[[i]]] == 0, 0, 
      Total[inf /@ Flatten@Position[mat[[i]], 1]]]);
influences = inf /@ Range@Length@mat - 1;
top3 = (Reverse@Sort@influences)[[;; 3]];
answer1 = StringJoin[ToString /@ top3]

Checking the answer to the second "hard" problem is actually easier than the first because you can use Mathematica's MIP solver. The problem basically asks for the smallest number of integers of several different type needed so that their sum adds up to a given total. Here's how you could do it in Mathematica

mintasks[total_] := (
   types = {2, 3, 17, 23, 42, 98};
   vars = x /@ Range@Length@types;
   poscons = And @@ (# >= 0 & /@ vars);
   First@Minimize[{Total[vars], vars.types == total && poscons}, vars,
      Integers]
   );
counts = mintasks /@ {2349, 2102, 2001, 1747};
answer2 = Times @@ counts

Chordal graph package update

I've fixed some bugs and added chordal-usage.nb (HTML) notebook with examples on how to do the following things with the chordal graph package:

- checking if the graph is chordal
- making graph chordal by adding fill edges using minimum fill heuristic
- getting perfect elimination ordering of a chordal graph
- arranging chordal matrix in perfect order
- arranging general sparse matrix in order that minimizes extra fill added by cholesky decomposition
- getting maximal cliques of a chordal graph
- getting clique tree structure of a chordal graph
- generating a chordal graph with given tree width and given tree structure

Description of methods is in Blair's excellent "An introduction to chordal graphs and clique trees" monograph


Chordal graphs release2

Chordal graph utilities

Here's visualization of a matrix and its Cholesky factorization



The sparsity pattern in the Cholesky factorization corresponds to the adjacency matrix of the graph triangulated using canonical ordering. This triangulation involves adding so called "fill" edges and can be visualized below




A matrix whose rows/columns can be symmetrically permuted to give Cholesky factorization with no extra fill cells is known as a "chordal" matrix, and a graph corresponding to that sparsity structure is known as chordal graph. Rearrangement of indices that produces factorization with no extra fill is known as "perfect elimination ordering".

Consider the following matrix and its Cholesky decomposition


This matrix is chordal, and perfect elimination ordering corresponds to reversing the order of rows/columns, here's the Cholesky decomposition with order reversed


When the matrix is not chordal, perfect elimination ordering is not possible, but you could still try to rearrange the indices to make result of symmetric Gaussian elimination as sparse as possible, this is known as min fill ordering. Greedy min-fill search will find perfect elimination ordering if one exists.

To arrange symmetric matrix A to make its Cholesky factorization as sparse as possible using greedy min fill search, do the following

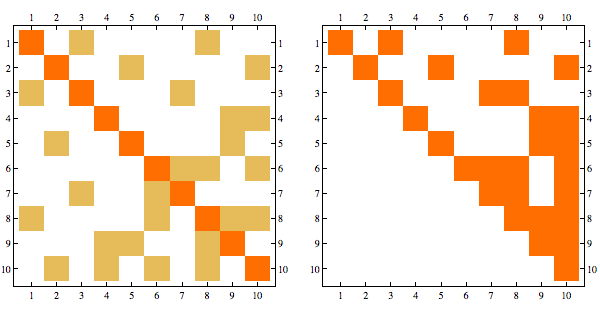
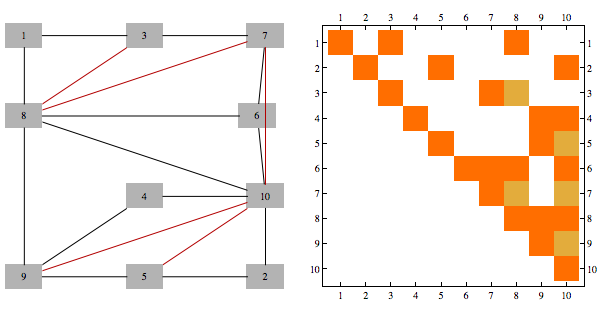
Needs{"Bulatov`chordal`"];
order = getMinFillOrder[AdjacencyGraph@Unitize@A];
CholeskyDecomposition[A[[Reverse@order, Reverse@order]]]

Here's an example of a structured sparse matrix and its Cholesky decomposition



Here's the result after randomly permuting indices


Using greedy minfill ordering we can recover some of the original structure


Here's a more complex example with non-linear structure



it's a matrix with sparsity pattern corresponding to the following graph



Randomly permuting indices we get the following



And here's the result in minfill order



Notebook
Packages

Cluster variation method example

Cluster variation methods for search work by approximating the distribution over satisfying instances, and then using marginals of that distribution to guide the search.

For instance, when trying to find largest independent set, you would specify probability distribution where probability of independent set k is proportional to lambda^size(k). As lambda goes to infinity, probability mass gets concentrated on nodes that are contained in the largest independent set

Here's an animation of occupation probability marginals with lambda going from 0 to 3. You can see the mass gets concentrated on nodes that are part of the largest independent set in the graph, at which point you can use greedy search


Notebook+packages

Making cross-words with Mathematica

A recent question on Stack Overflow asked how to use Mathematica to find a complete grid of words like this



Each row and each column must be a valid word.

A notebook below gives a way to solve this for small grids using SAT solver, and another answer in the post gives a pattern-based approach

Notebook

Listing all Hamiltonian cycles of the graph

You can encode Hamiltonian cycle problem into SAT. It's more complicated than independent sets in previous post, but it can be done by assigning number to each vertex indicating its position in Hamiltonian cycle, constraining chosen edges to be consistent with vertex numbering, and using SatisfiabilityInstances to find all satisfying assignments

Here are the 12 cycles produced this way for BislitCube


Here are the constraints that were used

• Every vertex has one incoming and one outgoing edge
  
• Cycles of length 2 are forbidden
  
• Every vertex is assigned one number
  
• First vertex is assigned number 1
  
• Presence of edge i,j implies number of number(j)=number(i)+1 and the converse
  

Smaller number of constraints can be used, but I found that increasing constraints makes SAT solver faster.

For these Graph Theory -> SAT encoding tasks, I find it helpful to have "formula"/ "vars" variables, and "decodeInstance"/"drawInstance" functions that so I can do something like this

sats = SatisfiabilityInstances[formula, vars, 20];
drawInstance /@ sats
decodeInstance /@ sats

decodeInstance turns variable assignment into readable/easy to process format, whereas drawInstance visualizes the instance as in pictures above.

Below is the notebook used to generate this diagram. It also has a helper .m file to draw a grid of all graphs with given set of properties. For instance, to show all graphs in GraphData that have 12 vertices, are Planar, Connected but are not Trees and fit in a 6x6 grid you would do

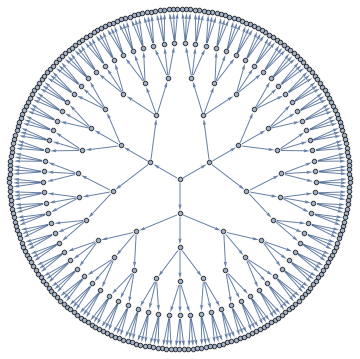
Needs["Bulatov`showGraphs`"];
showGraphs[12, "Connected", ! "Tree", "Planar", gridSize -> 6]

Name of graph shows up in Tooltip

Notebook+package

Using SAT solver to find independent sets

Here's a simple graph and all of its independent vertex sets



You can use SatisfiabilityInstances to get them as follows

gg = GridGraph[{2, 3}];
edge2clause[e_] := ! (e[[1]] && e[[2]]);
clauses = edge2clause /@ EdgeList[gg];
formula = And @@ clauses;
vars = VertexList[gg];
instances = SatisfiabilityInstances[formula, vars, 1000];
independentSets = Extract[vars, Position[#, True]] & /@ instances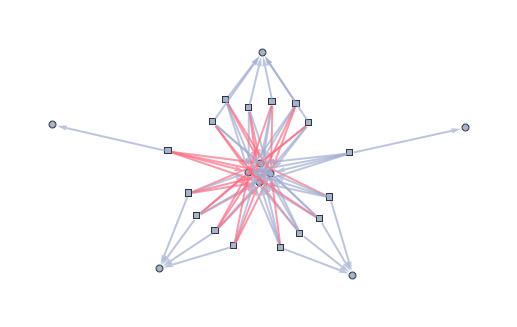

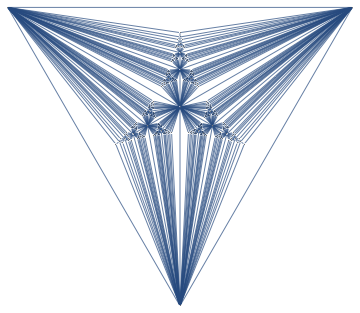
Notebook

Counters in SAT

Here's a visualization of a SAT formula of a BooleanCountingFunction. Four circles in the middle are the variables of interest. Five circles on the periphery are variables encoding the number of true assignments of the four circles in the middle. Squares are clauses, and color of the edge indicates whether the variable is negated in that clause. You can see from the color that rightmost circle represents "all variables are true" and leftmost circle represents "all variables are false".



Notebook

Tree decomposition package

A tree decomposition is a representation of a complete set of vertex separators of a graph. For instance, here's an Apollonian Network and its tree decomposition.




Decomposition above shows off 121 vertex separators of size 4, represented as non-leaf nodes, each separating graph into 3 parts, and 363 vertex separators of size 3, represented as edges, each separating the graph into 2 parts.

I put the tree decomposition code in a package. Unzip the file into any folder, and execute cells in treeDecomposition-usage.nb for the decomposition above. It takes 2 minutes for 367 vertex Apollonian network above. Graphs with around hundred vertices should take a few seconds.

Generally, to do a visualization like above, you'd do the following

<< Bulatov`treeDecomposition`;
g = GraphData[{"Apollonian", 5}];
{nodes, edges} = findTreeDecomposition[g];
GraphPlot[Rule @@@ edges]

Tree decomposition package

Coloring overlapping circles

Take some overlapping circles

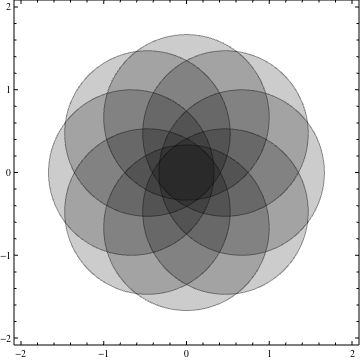
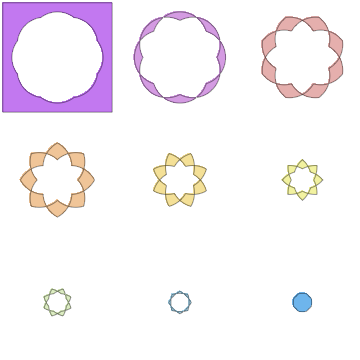
nc = 8;
ineqs = Table[(x - 2/3 Cos[i 2 Pi/nc])^2 + (y - 
        2/3 Sin[i 2 Pi/nc])^2 < 1, {i, 0, nc - 1}];
Show[Table[
  RegionPlot[ineqs[[k]], {x, -2, 2}, {y, -2, 2}, PlotPoints -> 35, 
   PlotStyle -> Opacity[.2]], {k, 1, nc}]]

What if we want to color overlapping regions according to how many overlaps they had?

We can use "BooleanCountingFunction" as follows

plots = Table[
   RegionPlot[
    BooleanCountingFunction[{k}, ineqs], {x, -2, 2}, {y, -2, 2}, 
    PlotPoints -> 100, Frame -> None, 
    PlotStyle -> ColorData["Pastel"][k/nc]], {k, 0, nc}];
GraphicsGrid@Partition[plots, 3]
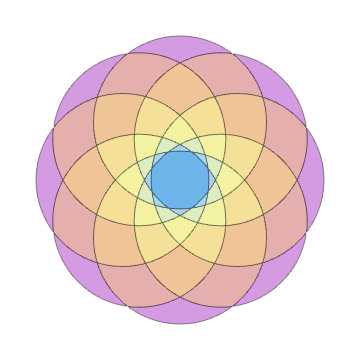
Show[Rest[plots]]

Independence Polynomials with Tree Decomposition

A lot of NP-hard problems on graphs become easy if you find a good tree decomposition of the graph.

Essentially, tree decomposition asks for a way to take a set of small sets of vertices and connect them in a way so that vertices shared by any pair of connected sets is a separator of the graph.

Two examples below show a graph on the left and it's optimal tree decomposition on the right






Following problems become easy once you have a good tree decomposition of a graph. Finding best: clique, independent set, dominating set, TSP tour, Steiner Tree. Almost every graph polynomial is tractable to compute given good tree decomposition. Finding BEST tree decomposition is NP-hard, but finding good decomposition is much easier. It parallelizes well, and simple heuristics give decompositions close to optimal for moderate size graphs even on my two-processor laptop.

Here are two relevant notebooks:

• Compute independence polynomials using tree decomposition
  
• Compute tree decomposition greedily and visualize it

Making Error Correcting code with FindIndependentVertexSet

Suppose you want to transmit information over a lossy channel. Your channel flips some bits at random and you want to choose your code-words so that you can recover the original codeword with high probability.

One approach is to pick a set of codewords of length n so that the Hamming distance between any two of them is at least d. This means that if the number of errors is less than (d-1)/2, you can recover the original word by picking code word closest in Hamming distance to the received word.

For example, for 3 bits and d=2, the code would be

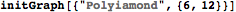
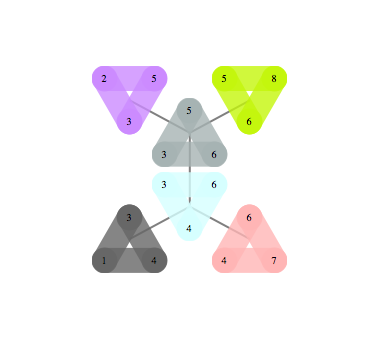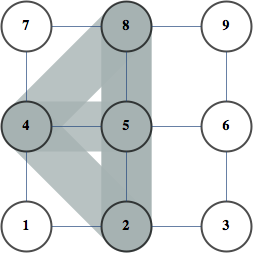100
010
001
111

Essentially when d=2, this is equivalent to finding a set of non-adjacent vertices of hypercube in n dimensions. For instance, code above can be visually represented as follows



For n=4 we can visualize it as follows


Essentially the problem is one of independent set, we construct a graph where vertices correspond to codewords and are connected if and only if hamming distance between them is 1.

Two graphs above correspond to "CubicalGraph" and "TesseractGraph" in GraphData, but if you want to recover the codewords, you want to control the ordering of vertices and construct the graph yourself. Getting the code is straightforward from the independent vertex set

words = Tuples[{0, 1}, 4];
distMat = Outer[HammingDistance, words, words, 1];
g = AdjacencyGraph[Map[Boole[# == 1] &, distMat, {2}]];
verts = FindIndependentVertexSet[g];
code = words[[verts]]

The result gives you a set of code-words over n-bits that are at least 2 bit flips apart from one another.

Now suppose we want to make our code more robust against errors. We construct graph as before, but augment it with the command "GraphPower[g,d-1]" to create a graph where vertices in an independent set are at least d steps apart. For n=6,d=2, VertexIndependentSet finds a code consisting of 8 codewords, which is the best possible.

It is known that for n=7,d=3 there's a code consisting of 16 codewords, although this problem seems to be too difficult to solve using version of VertexIndependentSet that ships with version 8.0

I'm experimenting with a message passing algorithm to solve this problem in the independent vertex set formulation, I'll post an update if it turns out better than the built-in

Notebook

Magic Square

Here's an interesting tidbit I saw linked from reddit -- the following decimal expansions form a magic square



Here's how you'd check the row and column sums

v = 18;
row[k_] := PadLeft[IntegerDigits[Floor[k/(v + 1)*10^v]], v];
mat = row /@ Range[v];
Total@mat
Total@Transpose@mat

Making web animations

I came across this cool animation on Sander Huisman's blog. Original animation was a lossy YouTube link, and it doesn't do it justice. The way to get a high-quality embedded animation is to generate individual frames and then export to Flash format as follows

Export["~/research/qr/hinges/anim.swf", images];

Then include the following snippet in your page. Location of the swf file goes in two places, allegedly to provide compatibility for IE+Mozilla browsers

Notebook