Computing Lovasz Theta function

One application of semi-definite programming is finding largest independent sets, or largest cliques in graph. According to Lovasz "Semidefinite programs and combinatorial optimization", SDP is the only known tractable way to find largest clique/independent set in perfect graphs.

One approach I've seen relies on the Lovasz theta function. Lovasz theta function is an estimate of independence number of the graph, and theta of graph's complement is guaranteed to lie between graphs's clique number and its chromatic number. Clique number and chromatic number are NP-complete, yet Lovasz theta function can be found in polynomial time using SDP. In perfect graphs and their complements, clique number and chromatic number coincide, which means that estimate from Lovasz theta function becomes exact.

I've put a function to compute Lovasz theta function using CVXOPT into package sdp2 below. You need to have CVXOPT and Pythonika installed as described here You could use it as follows

Install["/Users/Yaroslav/mathematica/Pythonika"];
SetDirectory[NotebookDirectory[]];
Needs["Bulatov`sdp2`"];
theta = lovaszTheta@GraphData[{"Paley", 13}];
RootApproximant@theta

This gives $\sqrt{13}$

Package also has a function "minimizeSpectralRadius" which finds matrix of smallest spectral radius subject to element constraints, and "lovaszComplete" which creates a graph by thresholding solution of "minimum spectral radius" formulation of Lovasz theta function (p.26 of Lovasz). Curiously, lovaszComplete reaches fixed point after 1 iteration for all graphs I tried --


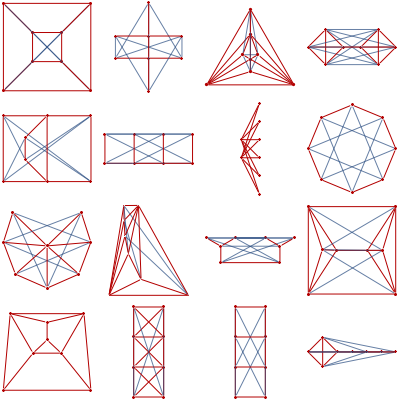
Red edges are original graph, blue are positive entries introduced when solving the SDP


SDP2 package