Independence Polynomials with Tree Decomposition

A lot of NP-hard problems on graphs become easy if you find a good tree decomposition of the graph.

Essentially, tree decomposition asks for a way to take a set of small sets of vertices and connect them in a way so that vertices shared by any pair of connected sets is a separator of the graph.

Two examples below show a graph on the left and it's optimal tree decomposition on the right






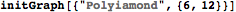
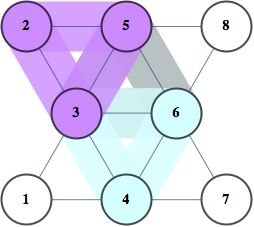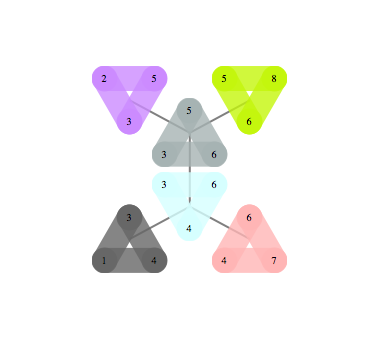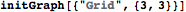
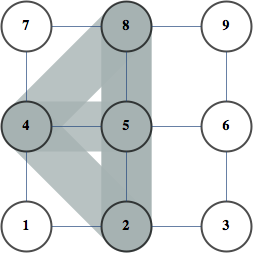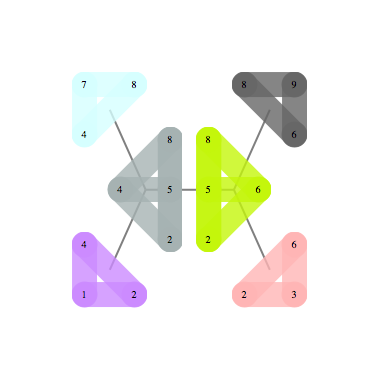Following problems become easy once you have a good tree decomposition of a graph. Finding best: clique, independent set, dominating set, TSP tour, Steiner Tree. Almost every graph polynomial is tractable to compute given good tree decomposition. Finding BEST tree decomposition is NP-hard, but finding good decomposition is much easier. It parallelizes well, and simple heuristics give decompositions close to optimal for moderate size graphs even on my two-processor laptop.

Here are two relevant notebooks:

• Compute independence polynomials using tree decomposition
  
• Compute tree decomposition greedily and visualize it