Plotting over 3d simplex

Someone on stackoverflow asked how to plot a function over 3d simplex.

I put together the code that takes care of rotations into "simplexPlot" and also used a recipe from math.SE for traditional 3D axes. Below is simplex plot of Sin[x y z]




The function "simplexPlot" in notebook plots the function in x-y plane. Function "axes" does traditional 3d axes. To visualize the connection to the original simplex domain, I rotate the whole plot back into original domain

t = AffineTransform[{{{-(1/Sqrt[2]), -(1/Sqrt[6]), 
      1/Sqrt[3]}, {1/Sqrt[2], -(1/Sqrt[6]), 1/Sqrt[3]}, {0, Sqrt[2/3],
       1/Sqrt[3]}}, {1/3, 1/3, 1/3}}];
graphics = simplexPlot[5 Sin[#1 #2 #3] &, Plot3D];
shape = Cases[graphics, _GraphicsComplex];
gr = Graphics3D[{Opacity[.5], GeometricTransformation[shape, t]}, 
   Axes -> False, Boxed -> False, Lighting -> "Neutral"];
Show[gr, axes[1, 1, 1, 0.05, 0.02]]

Notebook

Hyperpublic programming challenge

A start-up put up a small programming challenge.

There was some doubt whether the automatic answer key was correct, so I decided to check the answers using Mathematica. (note, it might be considered cheating to submit solutions obtained using Mathematica)

The first problem asks to find "influence" which comes down to the problem of counting descendants of each node in a graph, and can be done using recursion with memoization. Using Daniel Lichtblau's suggestion on how to parse the adjacency matrix, here's the whole solution.

words = ReadList["challenge2input.txt", Word];
mat = Map[Characters, words] /. {"O" -> 0, "X" -> 1};
inf[i_] := (inf[i] = 
    1 + If[Total[mat[[i]]] == 0, 0, 
      Total[inf /@ Flatten@Position[mat[[i]], 1]]]);
influences = inf /@ Range@Length@mat - 1;
top3 = (Reverse@Sort@influences)[[;; 3]];
answer1 = StringJoin[ToString /@ top3]

Checking the answer to the second "hard" problem is actually easier than the first because you can use Mathematica's MIP solver. The problem basically asks for the smallest number of integers of several different type needed so that their sum adds up to a given total. Here's how you could do it in Mathematica

mintasks[total_] := (
   types = {2, 3, 17, 23, 42, 98};
   vars = x /@ Range@Length@types;
   poscons = And @@ (# >= 0 & /@ vars);
   First@Minimize[{Total[vars], vars.types == total && poscons}, vars,
      Integers]
   );
counts = mintasks /@ {2349, 2102, 2001, 1747};
answer2 = Times @@ counts

Chordal graph package update

I've fixed some bugs and added chordal-usage.nb (HTML) notebook with examples on how to do the following things with the chordal graph package:

- checking if the graph is chordal
- making graph chordal by adding fill edges using minimum fill heuristic
- getting perfect elimination ordering of a chordal graph
- arranging chordal matrix in perfect order
- arranging general sparse matrix in order that minimizes extra fill added by cholesky decomposition
- getting maximal cliques of a chordal graph
- getting clique tree structure of a chordal graph
- generating a chordal graph with given tree width and given tree structure

Description of methods is in Blair's excellent "An introduction to chordal graphs and clique trees" monograph


Chordal graphs release2

Chordal graph utilities

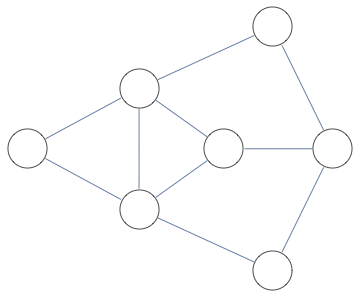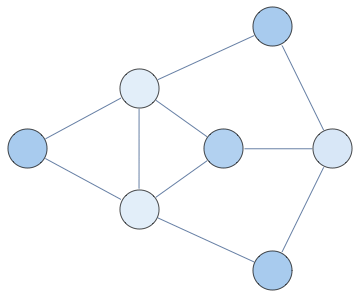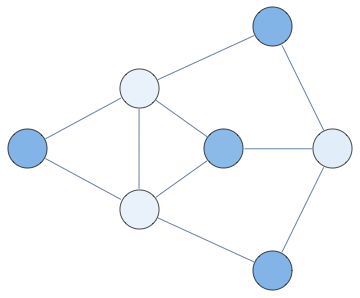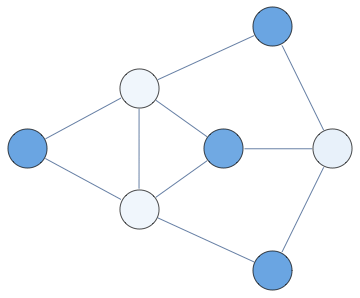
Here's visualization of a matrix and its Cholesky factorization



The sparsity pattern in the Cholesky factorization corresponds to the adjacency matrix of the graph triangulated using canonical ordering. This triangulation involves adding so called "fill" edges and can be visualized below




A matrix whose rows/columns can be symmetrically permuted to give Cholesky factorization with no extra fill cells is known as a "chordal" matrix, and a graph corresponding to that sparsity structure is known as chordal graph. Rearrangement of indices that produces factorization with no extra fill is known as "perfect elimination ordering".

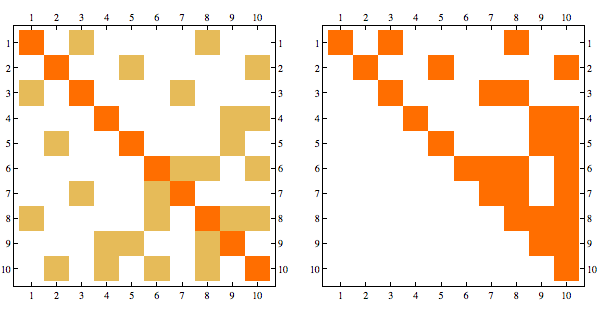
Consider the following matrix and its Cholesky decomposition


This matrix is chordal, and perfect elimination ordering corresponds to reversing the order of rows/columns, here's the Cholesky decomposition with order reversed


When the matrix is not chordal, perfect elimination ordering is not possible, but you could still try to rearrange the indices to make result of symmetric Gaussian elimination as sparse as possible, this is known as min fill ordering. Greedy min-fill search will find perfect elimination ordering if one exists.

To arrange symmetric matrix A to make its Cholesky factorization as sparse as possible using greedy min fill search, do the following

Needs{"Bulatov`chordal`"];
order = getMinFillOrder[AdjacencyGraph@Unitize@A];
CholeskyDecomposition[A[[Reverse@order, Reverse@order]]]

Here's an example of a structured sparse matrix and its Cholesky decomposition



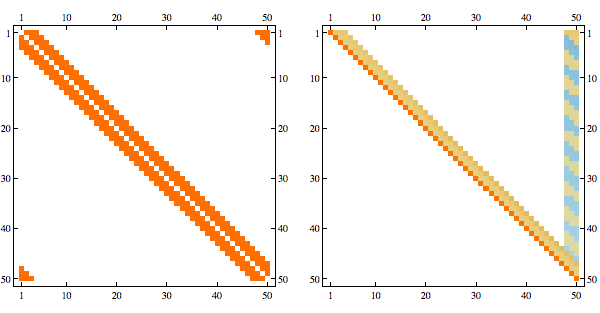
Here's the result after randomly permuting indices


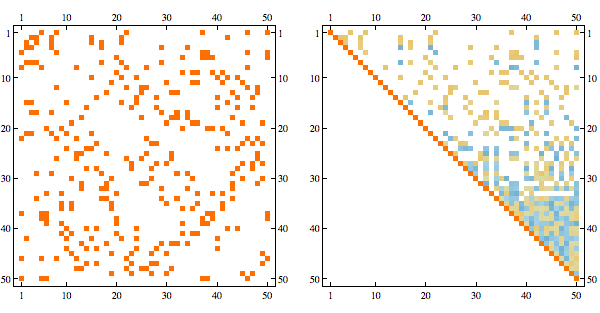
Using greedy minfill ordering we can recover some of the original structure


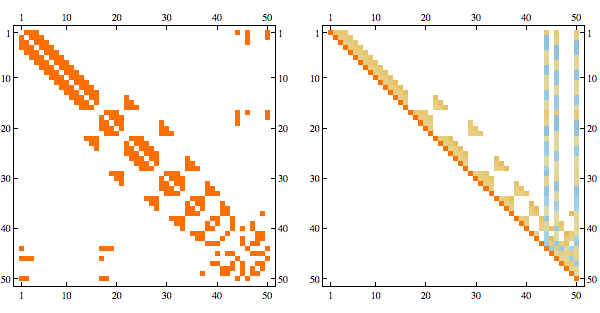
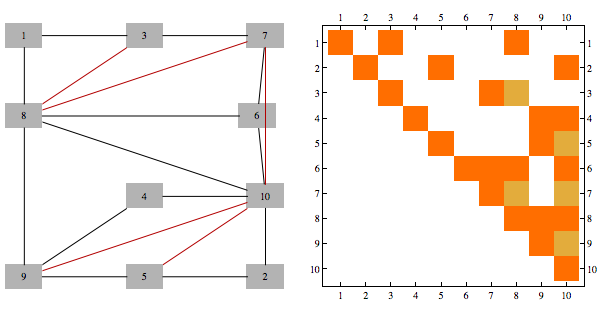
Here's a more complex example with non-linear structure



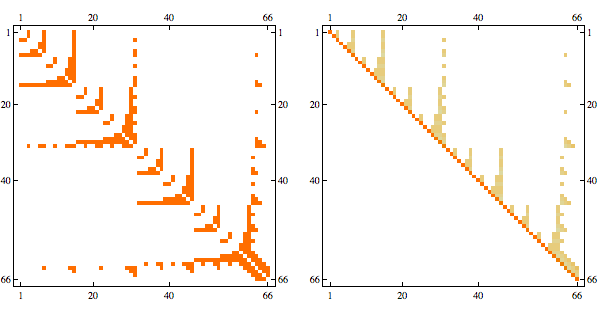
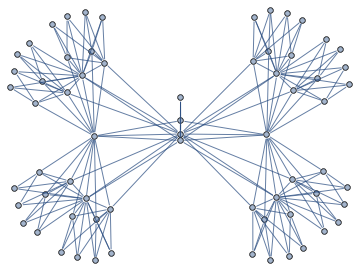
it's a matrix with sparsity pattern corresponding to the following graph



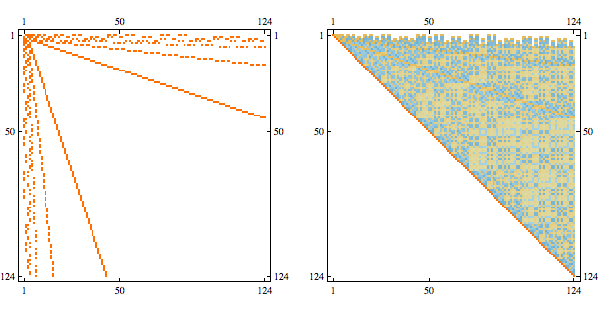
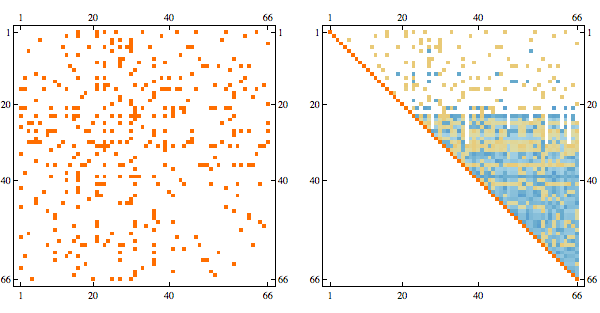
Randomly permuting indices we get the following



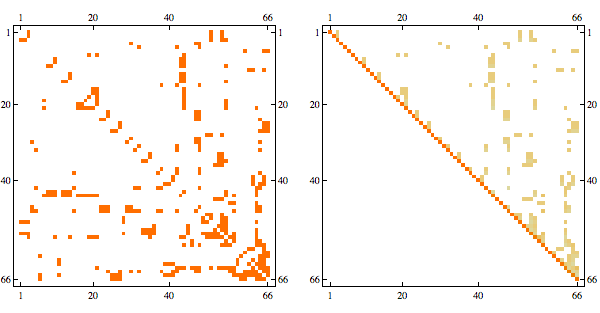
And here's the result in minfill order



Notebook
Packages

Cluster variation method example

Cluster variation methods for search work by approximating the distribution over satisfying instances, and then using marginals of that distribution to guide the search.

For instance, when trying to find largest independent set, you would specify probability distribution where probability of independent set k is proportional to lambda^size(k). As lambda goes to infinity, probability mass gets concentrated on nodes that are contained in the largest independent set

Here's an animation of occupation probability marginals with lambda going from 0 to 3. You can see the mass gets concentrated on nodes that are part of the largest independent set in the graph, at which point you can use greedy search


Notebook+packages

Making cross-words with Mathematica

A recent question on Stack Overflow asked how to use Mathematica to find a complete grid of words like this



Each row and each column must be a valid word.

A notebook below gives a way to solve this for small grids using SAT solver, and another answer in the post gives a pattern-based approach

Notebook