Making anti-aliased diagrams

Even though Mathematica supports anti-aliasing for 3D graphics, it's done inside the video-card which often make computational shortcuts and anti-aliasing quality is sub-optimal. A better way is to rasterize your diagram at higher resolution before exporting, as follows

is=360;
raster=Rasterize[graphic, ImageSize -> is, RasterSize -> 2 is];
Export["~/image.png",raster];

Notebook

How to get Mathematica help

Online sources:

• stack overflow: post your question and make sure to include "mathematica" in tags. This is the fastest way and usually you get an answer within 30 minutes. A couple of WRI employees occasionally answer questions there.
  
  
• Mathematica newsgroup: if you are willing to wait a day for the answer, it can be helpful. Questions containing explicit mentions of competing systems will be rejected, so if you have a question along the lines of "I need to implement an equivalent of OrbitsDomain in GAP", you need to say "I need a function that works similar to OrbitsDomain in a certain open-source group theory package". I usually turn to newsgroup when the stackoverflow community can not answer, and have occasionally gotten very insightful responses.
  
  
• Math stack exchange: use it when your question has significant math component and use "mathematica" tag. Answer will possibly tell you how to do this in some other system
  

Eventually there may be a separate stack exchange for Mathematica users. The proposal is here and the number of followers has been steadily going up.


It helps to include self-contained piece of code in your question illustrating the issue.

Two guidelines:

• Make sure your code works on fresh kernel
  
• Search the forum for your question before asking it
  

Visualizing 7 dimensional simplex

One way to visualize a 7 dimensional simplex is to plot sections of it. You could restrict attention to (hyper)plane sections that go through points defined by averaging some set of vertices, and discard geometrically identical ones. There are only two such sections for 3d simplex



For 7d simplex, there are 49 such sections, and the most symmetrical one is the octahedron, which in the notebook below was found as the set of all 8 dimensional unit vectors with non-negative components orthogonal to (0, 3, 1, 0, -5, 0, 0, 1)


Here are all 49 distinct sections


Complete code is here.
An outline of how they were generated:

• Use Peter Shor's observation that there's a homomorphism between distinct sections and ways to assign 8 identical objects to vertices of the cube
  
• Find such permutations by breaking space of all permutations of 8 objects into orbits under action of group of cube rotations and taking one representative from each orbit, using PermutationGroup, GroupElements and Permute, implemented as nonEquivalentPermutations
  
• Use BooleanCounting function and SatisfiabilityInstances to find assignment of vertices to centroids consistent with given cube representation, implemented as findAssignment
  
• Use NullSpace, Reduce and FindInstances to find 0-dimensional intersections of hyperplane defining the section with some subset of 8 simplex cells, implemented as getExtremePoints and getCons
  
• Those point sets define vertices of the section, use SingularValueDecomposition to find vertex sets with distinct sets of four non-zero singular values, implemented as singularCert and distinctPoses
  
• Project distinct point sets onto hyperplane defining the section and use ComputationalGeometry`Methods`ConvexHull3D to get description of the shape in terms of polygons, implemented as getVerts3D and getPoly
  

Notebook

Group theory bits

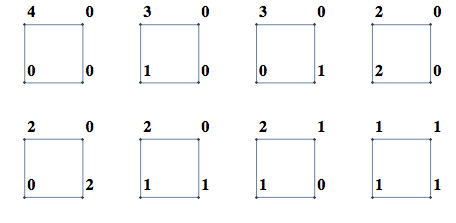
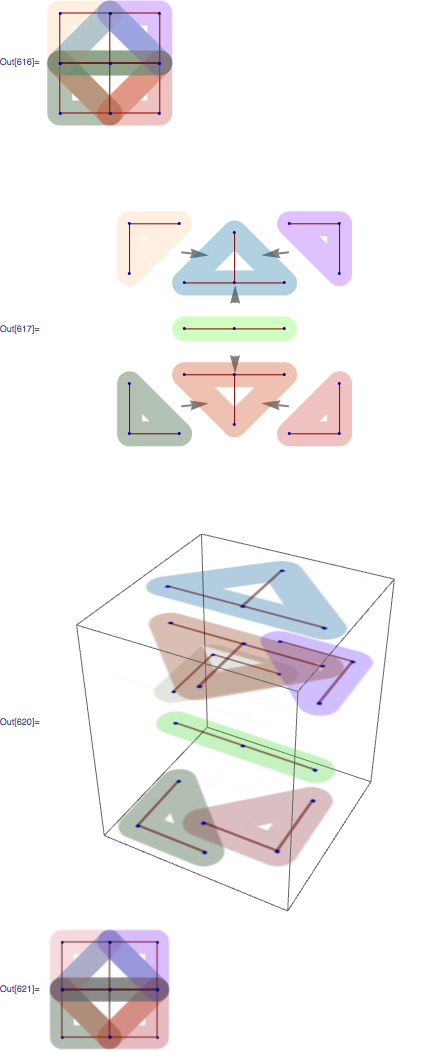
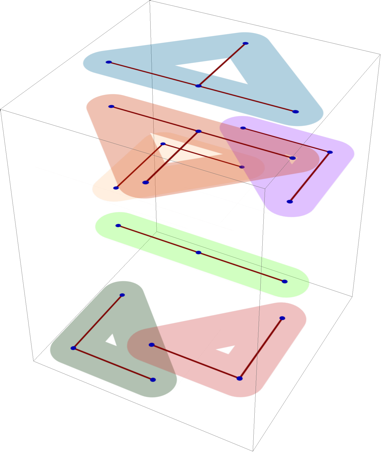
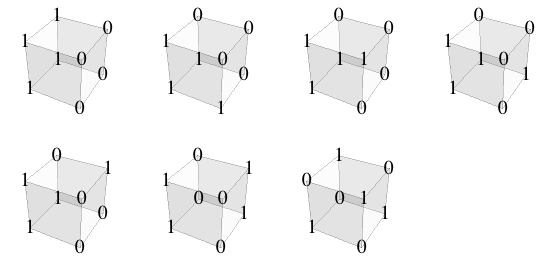
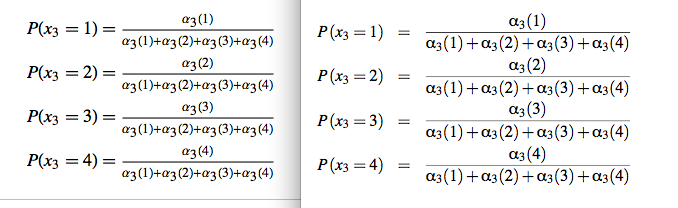Suppose we want to get the number of ways of assigning 4 zeros and 4 ones to vertices of the cube, distinct under rotations of the cube. We can use similar approach as in the previous post, and while the relevant group of symmetry is not built into Mathematica, we can construct it manually from generators. Consider two rotations of the cube, one around vertical axis and another around horizontal



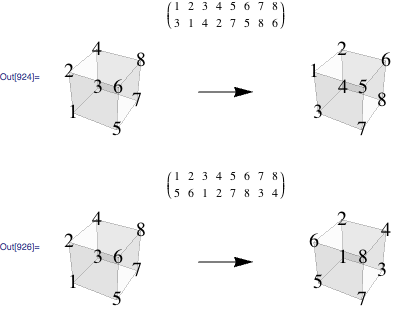
You can specify this group using generators above as permutation lists follows

group1=PermutationGroup[PermutationCycles /@ {{3, 1, 4, 2, 7, 5, 8, 6},{5, 6, 1, 2, 7, 8, 3, 4}}];

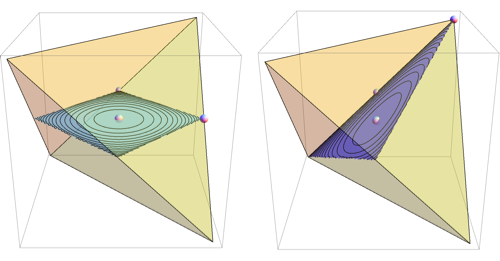
Note, that there's more than one way to specify group using generators and they produce non-isomorphic Cayley graphs. Here are two more representations of the group above

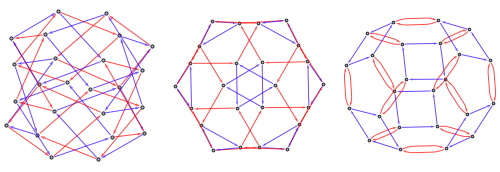
group2 = PermutationGroup[
   PermutationCycles /@ {{3, 1, 4, 2, 7, 5, 8, 6}, {7, 5, 3, 1, 8, 6, 
      4, 2}}];
group3 = SymmetricGroup[4];
CayleyGraph /@ {group1, group2, group3} // 
 GraphicsRow

group2 uses rotation around axis through center of two faces and another rotation around long diagonal. This group is known to be isomorphic to the SymmetricGroup[4], so group3 uses standard generators of that group.


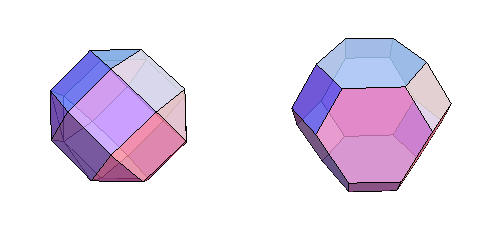
The last two graphs are planar so you plot them in 3D as polyhedra



To generate all permutations of {1,1,1,1,0,0,0,0}, you could take a list of all permutations and weed out permutations identical under action of group1 or group2, using method from previous post. Even though group3 is isomorphic to our group, it's not represented as a subgroup of SymmetricGroup[8], so to use that method, we'd need to identify it as a subgroup of Symmetric Group[8]. We can do that by finding that a pi and 2pi/3 rotations of cube into itself. One axis is the long diagonal, and another goes through center of cube and centers of two cube edges, which gives the following representation

PermutationGroup[Cycles /@ {{{1, 2, 4, 3}, {5, 6, 8, 7}}, {{6, 3}, {5, 4}, {1, 2}, {7,8}}}]

Here are the resulting 7 permutations



Notebook

Partitioning integer among vertices of square

You can use "IntegerPartitions" to find all ways to partition integer when order doesn't matter, and you can combine it with Permutations to get list when the order matters. What if the order *kind of* matters?

More concretely, suppose you want to generate ways to break 4 among vertices of a square. Since the square is symmetric under rotations and flips, we end up with 8 ways.


Symmetries of the square are represented by the 4th order dihedral group, so you could start with all permutations of integer partitions of 4 and then use Mathematica 8.0's Permute and GroupElements to weed out equivalent permutations as follows

(* remove group elements except the one given from list *)
removeEquivalent[list_, item_, group_] := (
  equivalents = Permute[item, #] & /@ GroupElements[group];
  DeleteCases[list, Alternatives @@ equivalents]
  )
list = {{1, 2, 3, 4}, {3, 2, 1, 4}, {2, 1, 3, 4}};
removeEquivalent[list, First[list], DihedralGroup[4]]

Same approach works to for similar problem in 3 dimensions, but too slow for 4 dimensions

notebook

Mathematica + Python

Here's an extension that seems useful if you use both Python and Mathematica. I haven't yet tested it, but probably will soon.
http://dkbza.org/pythonika.html

Mathematica's Graph classes

Notebook attached shows how to do the following:

1. Generate diagram of relationships implied by 5000 graphs in Mathematica's GraphData
2. Test membership of 7 classes using built-in methods and 6 additional classes using Combinatorica methods
3. Find name of graph in GraphData collection using membership tests above and IsomorphicGraphQ

Image

Notebook

Tiles with holes

You can use Thickness, Line, JoinForm["Round"] and CapForm["Round"] to create aesthetically pleasing tiles as in previous posts, but what if you want them to be hollow? One approach is to draw two sets of tiles, large and small, then use Rasterize and overlay small tiles onto the alpha channel to make those areas transparent.

Keep in mind that this method is quite slow, it takes 20 seconds to render the image below. For a more efficient approach, you may need to use "Image"



The code to generate it is below. It's more complicated than needed for a simple diagram above because it's designed to allow branching tiles like here

Notebook

FindSequenceFunction

I stumbled onto this on accident since it's not advertised much. You can extract the pattern in the sequence using

FindSequenceFunction[{20, 24, 28, 32, 36, 40}]

New in version 7. This functionality is one of the reasons I used Maple several years ago.
A related function is "RootApproximant" which tries to find an algebraic number approximating a given real.

Here's a tricky one -- number of regions in 4-space formed by n-1 hyperplanes. It starts with

1,2,4,8,16

Mathematica incorrectly guesses 2^n



Next term of the sequence is 31, if you include that term, it gives the correct formula

Real-life graphs collection in Mathematica

Type ExampleData["NetworkGraph"] to get the list
Some of them seem to be mentioned in tutorial/GraphDrawing
And others on what's new in Mathematica 8

Mathematica-related blogs

Wolfram posts links to online coverage

Also these blogs seem to talk about Mathematica
http://scienceblogs.com/builtonfacts/
http://blog.keksrolle.de
http://mathgis.blogspot.com/
http://mathplugged.blogspot.com/
http://www.mathgeek.com/
http://nylander.wordpress.com
http://pragma.posterous.com
http://rip94550.wordpress.com
http://semanticvector.blogspot.com/
http://thinkmeta.wordpress.com
http://ubpdqn.wordpress.com

New in version 8.0

Texture

You can use Texture to take 2D diagrams into 3D, like below



If you want original colors and higher quality, use Lighting->"Neutral" and Rasterize the texture at 4x resolution




Notebook

Enumerating and generating combinations of symbols

1. Order doesn't matter, repetition not allowed

Enumerating: Subsets, Sampling: ???

2. Order doesn't matter, repetition allowed
Enumerating: IntegerPartition followed by Permutations followed by mapping counts into symbols , Sampling: ???

3. Order matters, repetition not allowed:
Enumerating: Permutations@Subsets, Sampling: RandomSample

4. Order matters, repetition allowed:
Enumerating: Tuples, Sampling: RandomChoice

Mathematica vs Latex

Can you guess which is which?