Chordal graph utilities

Here's visualization of a matrix and its Cholesky factorization



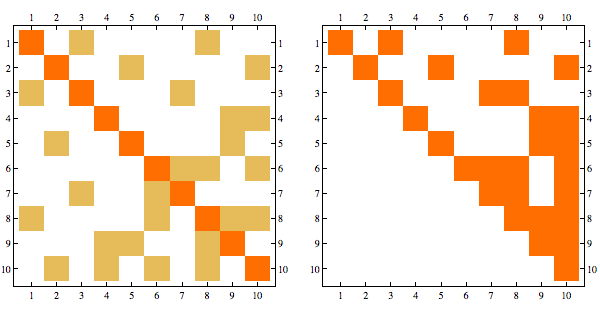
The sparsity pattern in the Cholesky factorization corresponds to the adjacency matrix of the graph triangulated using canonical ordering. This triangulation involves adding so called "fill" edges and can be visualized below




A matrix whose rows/columns can be symmetrically permuted to give Cholesky factorization with no extra fill cells is known as a "chordal" matrix, and a graph corresponding to that sparsity structure is known as chordal graph. Rearrangement of indices that produces factorization with no extra fill is known as "perfect elimination ordering".

Consider the following matrix and its Cholesky decomposition


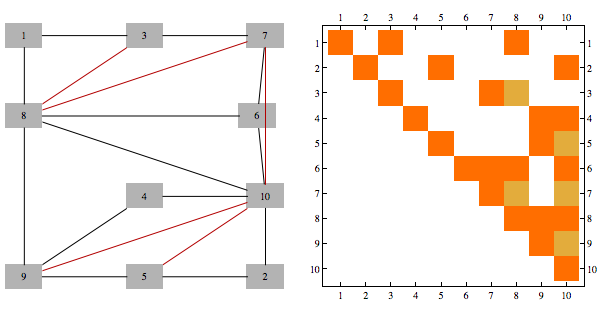
This matrix is chordal, and perfect elimination ordering corresponds to reversing the order of rows/columns, here's the Cholesky decomposition with order reversed


When the matrix is not chordal, perfect elimination ordering is not possible, but you could still try to rearrange the indices to make result of symmetric Gaussian elimination as sparse as possible, this is known as min fill ordering. Greedy min-fill search will find perfect elimination ordering if one exists.

To arrange symmetric matrix A to make its Cholesky factorization as sparse as possible using greedy min fill search, do the following

Needs{"Bulatov`chordal`"];
order = getMinFillOrder[AdjacencyGraph@Unitize@A];
CholeskyDecomposition[A[[Reverse@order, Reverse@order]]]

Here's an example of a structured sparse matrix and its Cholesky decomposition



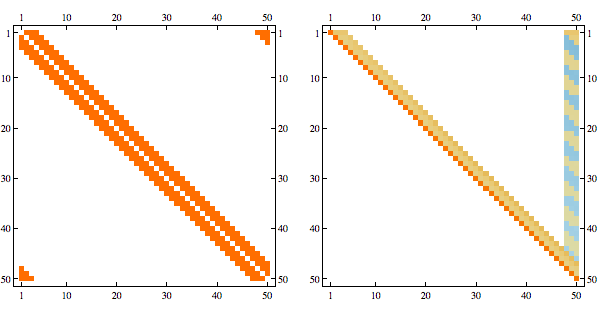
Here's the result after randomly permuting indices


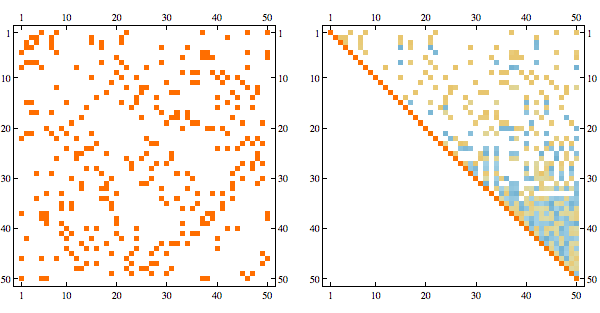
Using greedy minfill ordering we can recover some of the original structure


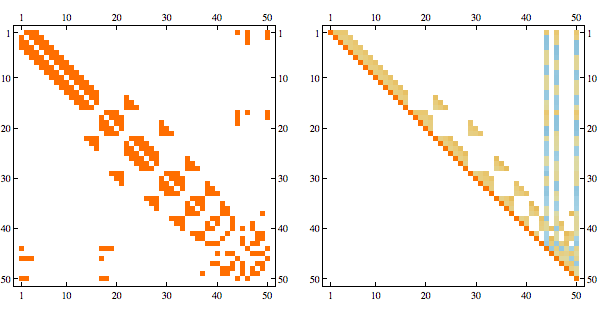
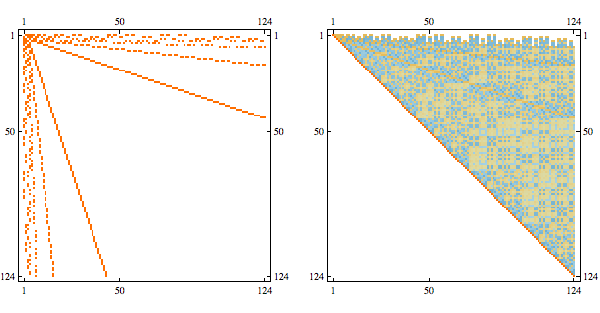
Here's a more complex example with non-linear structure



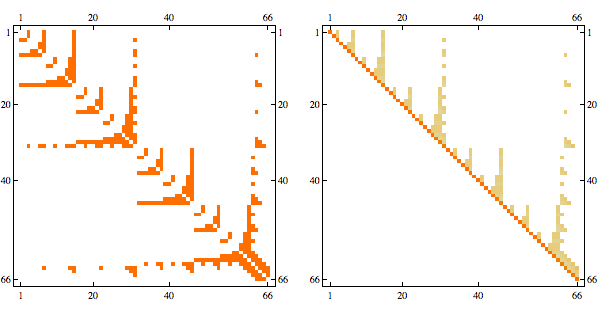
it's a matrix with sparsity pattern corresponding to the following graph



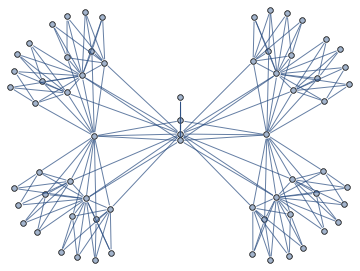
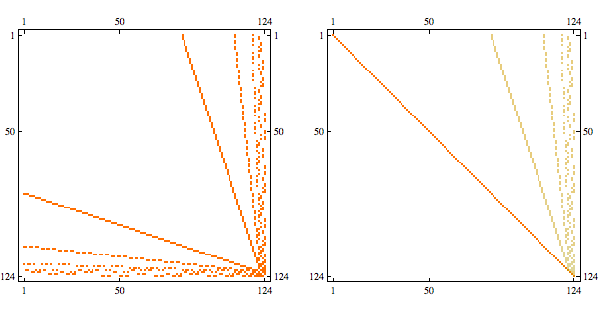
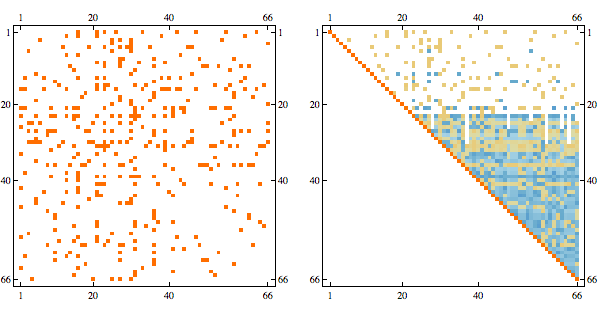
Randomly permuting indices we get the following



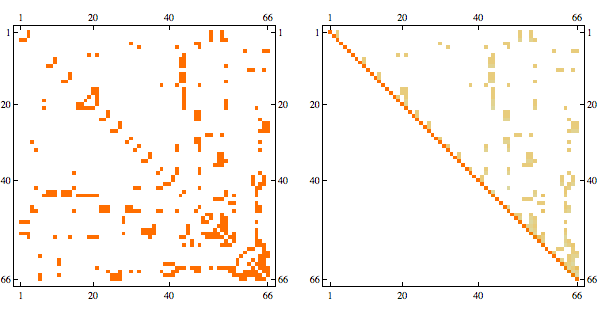
And here's the result in minfill order



Notebook
Packages