There's a number of graph utilities and tricks I use when working with graphs in Mathematica 8, I've summarized them in notebook graphUsage.nb. You can get this notebook and all required packages here.
Brief overview:
Fixing annoyances
programmatically changing style of existing graph, modifying graphs without forgetting vertex coordinates, using GraphPlot's layout for Graph objects, aligning adjacency matrix with vertex labels in index graphs
Listing graph structures
cliques, independent sets, maximal cliques, maximal independent sets, hamiltonian circuits
Visualizing graphs
Showing all graphs that miss particular properties, visualizing graphs with intensity attached to vertices -- pieGraph and fadedGraph. Showing graph with several types of vertices.
Friday, March 25, 2011
Thursday, March 3, 2011
Computing Lovasz Theta function
One application of semi-definite programming is finding largest independent sets, or largest cliques in graph. According to Lovasz "Semidefinite programs and combinatorial optimization", SDP is the only known tractable way to find largest clique/independent set in perfect graphs.
One approach I've seen relies on the Lovasz theta function. Lovasz theta function is an estimate of independence number of the graph, and theta of graph's complement is guaranteed to lie between graphs's clique number and its chromatic number. Clique number and chromatic number are NP-complete, yet Lovasz theta function can be found in polynomial time using SDP. In perfect graphs and their complements, clique number and chromatic number coincide, which means that estimate from Lovasz theta function becomes exact.
I've put a function to compute Lovasz theta function using CVXOPT into package sdp2 below. You need to have CVXOPT and Pythonika installed as described here You could use it as follows
This gives $\sqrt{13}$
Package also has a function "minimizeSpectralRadius" which finds matrix of smallest spectral radius subject to element constraints, and "lovaszComplete" which creates a graph by thresholding solution of "minimum spectral radius" formulation of Lovasz theta function (p.26 of Lovasz). Curiously, lovaszComplete reaches fixed point after 1 iteration for all graphs I tried --
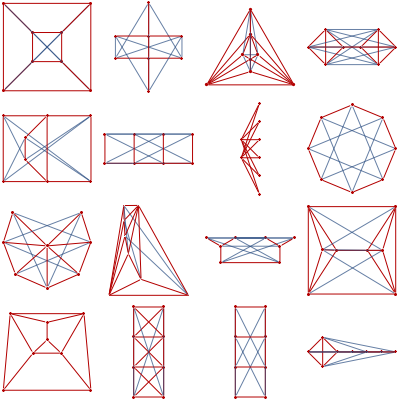
Red edges are original graph, blue are positive entries introduced when solving the SDP

SDP2 package
One approach I've seen relies on the Lovasz theta function. Lovasz theta function is an estimate of independence number of the graph, and theta of graph's complement is guaranteed to lie between graphs's clique number and its chromatic number. Clique number and chromatic number are NP-complete, yet Lovasz theta function can be found in polynomial time using SDP. In perfect graphs and their complements, clique number and chromatic number coincide, which means that estimate from Lovasz theta function becomes exact.
I've put a function to compute Lovasz theta function using CVXOPT into package sdp2 below. You need to have CVXOPT and Pythonika installed as described here You could use it as follows
Install["/Users/Yaroslav/mathematica/Pythonika"];
SetDirectory[NotebookDirectory[]];
Needs["Bulatov`sdp2`"];
theta = lovaszTheta@GraphData[{"Paley", 13}];
RootApproximant@theta
This gives $\sqrt{13}$
Package also has a function "minimizeSpectralRadius" which finds matrix of smallest spectral radius subject to element constraints, and "lovaszComplete" which creates a graph by thresholding solution of "minimum spectral radius" formulation of Lovasz theta function (p.26 of Lovasz). Curiously, lovaszComplete reaches fixed point after 1 iteration for all graphs I tried --

Red edges are original graph, blue are positive entries introduced when solving the SDP

SDP2 package
Semidefinite programming in Mathematica using CVXOPT
One can get access to semidefinite programming from Mathematica by using Pythonika to interface with Python's cvxopt package.
For MacOS 10.6 and Mathematica 8 the following should work
If your compilation doesn't work, post a follow-up comment here
Then you can use my package Bulatov`sdp1 to get direct access to one common form of SDP -- maximize a linear function of a matrix subject to positive-definiteness and element value constraints.
As an example application, consider MAXCUT -- find partition of the vertices such that number of edges connecting vertices from different partitions is maximized.
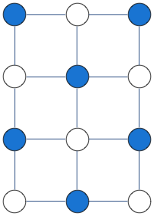
Solution above was obtained by solving a binary integer quadratic program, as follows
SDP relaxation gives a guaranteed approximation to binary quadratic program above --
This gives the same solution for the example above, but is much faster. solveDualSDP here finds psd matrix X that maximizes -A.X with diagonal entries of X constrained to be 1. For more details on this formulation, see Chapter 6 of Williamson,Shmoys, Design of Approximation Algorithms. For details of how to convert SDPs to standard vectorized form as used by CVXOPT, see this post

Packages
Notebook
For MacOS 10.6 and Mathematica 8 the following should work
- Install 64-bit Python 2.7 distribution from official site
- Get latest cvxopt sources and make
- Get Pythonika sources from google site
- copy mathlink.framework (in /Applications/Mathematica.app/SystemFiles/Links/MathLink/DeveloperKit/CompilerAdditions/) to /Library/Frameworks directory
- Fill correct paths in Pythonika Makefile, also add "-lstdc++ -framework CoreFoundation" linker flags
- In Pythonika Makefile, rename libML.a into libMLi3.a
If your compilation doesn't work, post a follow-up comment here
Then you can use my package Bulatov`sdp1 to get direct access to one common form of SDP -- maximize a linear function of a matrix subject to positive-definiteness and element value constraints.
As an example application, consider MAXCUT -- find partition of the vertices such that number of edges connecting vertices from different partitions is maximized.

Solution above was obtained by solving a binary integer quadratic program, as follows
g = GridGraph[{4, 3}];
A = AdjacencyMatrix@g;
n = Length@VertexList@g;
u = ConstantArray[1, n];
vars = x /@ Range@n;
cons = And @@ (-1 <= x[#] <= 1 & /@ Range@n);
solution=vars /. Last[Maximize[{-vars.A.vars, cons}, vars, Integers]]SDP relaxation gives a guaranteed approximation to binary quadratic program above --
Needs["Bulatov`sdp1`"];
Install["/Users/Yaroslav/mathematica/Pythonika"];
gram = solveDualSDP[-A, IdentityMatrix[n], u];
solution = gramRound[gram];
This gives the same solution for the example above, but is much faster. solveDualSDP here finds psd matrix X that maximizes -A.X with diagonal entries of X constrained to be 1. For more details on this formulation, see Chapter 6 of Williamson,Shmoys, Design of Approximation Algorithms. For details of how to convert SDPs to standard vectorized form as used by CVXOPT, see this post

Packages
Notebook
Subscribe to:
Posts (Atom)