Semidefinite programming in Mathematica using CVXOPT

One can get access to semidefinite programming from Mathematica by using Pythonika to interface with Python's cvxopt package.

For MacOS 10.6 and Mathematica 8 the following should work

• Install 64-bit Python 2.7 distribution from official site
  
• Get latest cvxopt sources and make
  
• Get Pythonika sources from google site
  
• copy mathlink.framework (in /Applications/Mathematica.app/SystemFiles/Links/MathLink/DeveloperKit/CompilerAdditions/) to /Library/Frameworks directory
  
• Fill correct paths in Pythonika Makefile, also add "-lstdc++ -framework CoreFoundation" linker flags
  
• In Pythonika Makefile, rename libML.a into libMLi3.a
  

If your compilation doesn't work, post a follow-up comment here

Then you can use my package Bulatov`sdp1 to get direct access to one common form of SDP -- maximize a linear function of a matrix subject to positive-definiteness and element value constraints.

As an example application, consider MAXCUT -- find partition of the vertices such that number of edges connecting vertices from different partitions is maximized.



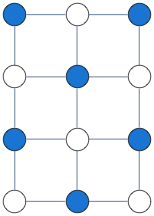
Solution above was obtained by solving a binary integer quadratic program, as follows

g = GridGraph[{4, 3}];
A = AdjacencyMatrix@g;
n = Length@VertexList@g;
u = ConstantArray[1, n];
vars = x /@ Range@n;
cons = And @@ (-1 <= x[#] <= 1 & /@ Range@n);
solution=vars /. Last[Maximize[{-vars.A.vars, cons}, vars, Integers]]

SDP relaxation gives a guaranteed approximation to binary quadratic program above --

Needs["Bulatov`sdp1`"];
Install["/Users/Yaroslav/mathematica/Pythonika"];
gram = solveDualSDP[-A, IdentityMatrix[n], u];
solution = gramRound[gram];

This gives the same solution for the example above, but is much faster. solveDualSDP here finds psd matrix X that maximizes -A.X with diagonal entries of X constrained to be 1. For more details on this formulation, see Chapter 6 of Williamson,Shmoys, Design of Approximation Algorithms. For details of how to convert SDPs to standard vectorized form as used by CVXOPT, see this post



Packages
Notebook