Tree decomposition package

A tree decomposition is a representation of a complete set of vertex separators of a graph. For instance, here's an Apollonian Network and its tree decomposition.




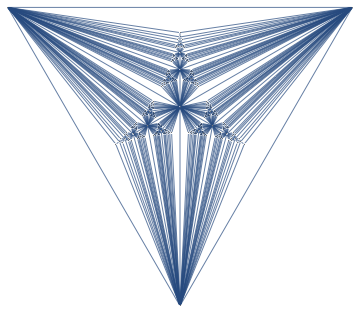
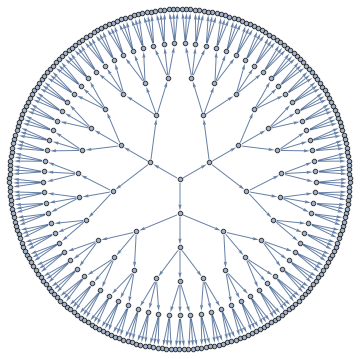
Decomposition above shows off 121 vertex separators of size 4, represented as non-leaf nodes, each separating graph into 3 parts, and 363 vertex separators of size 3, represented as edges, each separating the graph into 2 parts.

I put the tree decomposition code in a package. Unzip the file into any folder, and execute cells in treeDecomposition-usage.nb for the decomposition above. It takes 2 minutes for 367 vertex Apollonian network above. Graphs with around hundred vertices should take a few seconds.

Generally, to do a visualization like above, you'd do the following

<< Bulatov`treeDecomposition`;
g = GraphData[{"Apollonian", 5}];
{nodes, edges} = findTreeDecomposition[g];
GraphPlot[Rule @@@ edges]

Tree decomposition package