Partitioning integer among vertices of square

You can use "IntegerPartitions" to find all ways to partition integer when order doesn't matter, and you can combine it with Permutations to get list when the order matters. What if the order *kind of* matters?

More concretely, suppose you want to generate ways to break 4 among vertices of a square. Since the square is symmetric under rotations and flips, we end up with 8 ways.


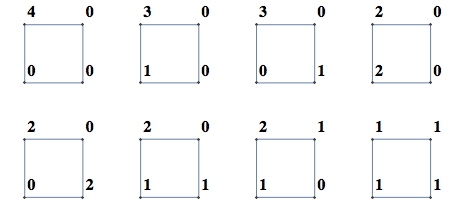
Symmetries of the square are represented by the 4th order dihedral group, so you could start with all permutations of integer partitions of 4 and then use Mathematica 8.0's Permute and GroupElements to weed out equivalent permutations as follows

(* remove group elements except the one given from list *)
removeEquivalent[list_, item_, group_] := (
  equivalents = Permute[item, #] & /@ GroupElements[group];
  DeleteCases[list, Alternatives @@ equivalents]
  )
list = {{1, 2, 3, 4}, {3, 2, 1, 4}, {2, 1, 3, 4}};
removeEquivalent[list, First[list], DihedralGroup[4]]

Same approach works to for similar problem in 3 dimensions, but too slow for 4 dimensions

notebook