Group theory bits

Suppose we want to get the number of ways of assigning 4 zeros and 4 ones to vertices of the cube, distinct under rotations of the cube. We can use similar approach as in the previous post, and while the relevant group of symmetry is not built into Mathematica, we can construct it manually from generators. Consider two rotations of the cube, one around vertical axis and another around horizontal



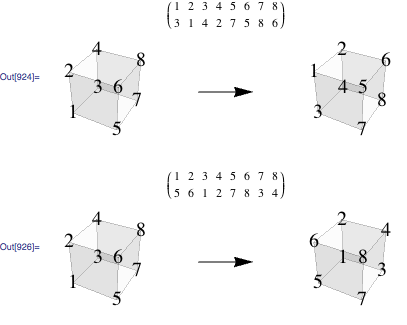
You can specify this group using generators above as permutation lists follows

group1=PermutationGroup[PermutationCycles /@ {{3, 1, 4, 2, 7, 5, 8, 6},{5, 6, 1, 2, 7, 8, 3, 4}}];

Note, that there's more than one way to specify group using generators and they produce non-isomorphic Cayley graphs. Here are two more representations of the group above

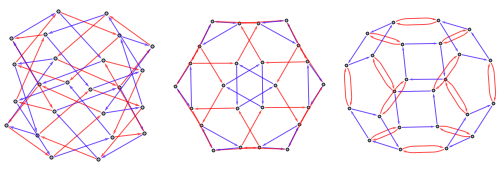
group2 = PermutationGroup[
   PermutationCycles /@ {{3, 1, 4, 2, 7, 5, 8, 6}, {7, 5, 3, 1, 8, 6, 
      4, 2}}];
group3 = SymmetricGroup[4];
CayleyGraph /@ {group1, group2, group3} // 
 GraphicsRow

group2 uses rotation around axis through center of two faces and another rotation around long diagonal. This group is known to be isomorphic to the SymmetricGroup[4], so group3 uses standard generators of that group.


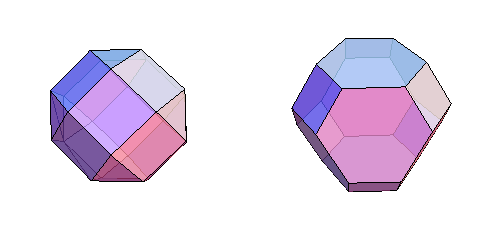
The last two graphs are planar so you plot them in 3D as polyhedra



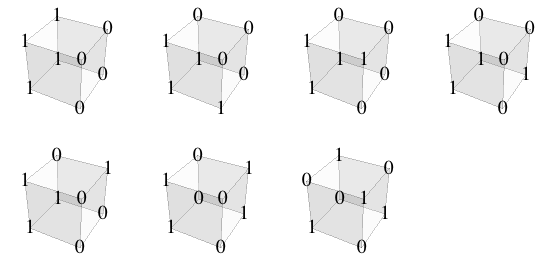
To generate all permutations of {1,1,1,1,0,0,0,0}, you could take a list of all permutations and weed out permutations identical under action of group1 or group2, using method from previous post. Even though group3 is isomorphic to our group, it's not represented as a subgroup of SymmetricGroup[8], so to use that method, we'd need to identify it as a subgroup of Symmetric Group[8]. We can do that by finding that a pi and 2pi/3 rotations of cube into itself. One axis is the long diagonal, and another goes through center of cube and centers of two cube edges, which gives the following representation

PermutationGroup[Cycles /@ {{{1, 2, 4, 3}, {5, 6, 8, 7}}, {{6, 3}, {5, 4}, {1, 2}, {7,8}}}]

Here are the resulting 7 permutations



Notebook