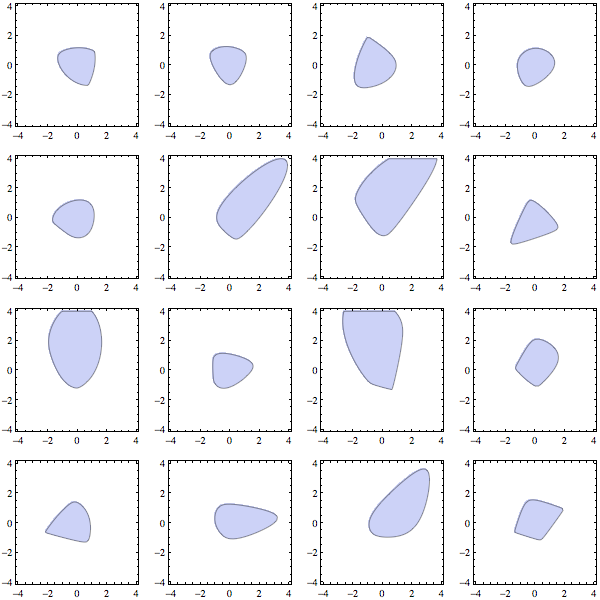
spectro13 := (
X = ( {
{x1, x2, x3, x7},
{x2, x4, x5, x8},
{x3, x5, x6, x9},
{x7, x8, x9, x10}
} );
vars = Union@Flatten@X;
dvars = {x, y};
m = Length@vars;
n = Length@dvars;
makeMat := X /. (Thread[vars -> #]) &;
proj = makeMat /@ Orthogonalize@RandomReal[{-1, 1}, {n, m}];
mat2 = Total@MapThread[Times, {proj, dvars}, 1] +
IdentityMatrix@Length@X;
cons = And @@ (Thread[Eigenvalues[mat2] >= 0]);
RegionPlot[cons, {x, -4, 4}, {y, -4, 4}, PlotPoints -> 15]
);
GraphicsGrid[Table[spectro13, {3}, {3}], ImageSize -> 600]
It doesn't look as instructive in 3D, but for example of doing the same in 3D, see this Mathematica stackexchange post
Very cool! I have a couple questions:
ReplyDelete1. Why do you add the identity matrix when defining mat2? Doesn't that make a matrix whose eigenvalues are too big (each too big by 1)?
2. In what sense are the two matrices in proj orthogonal? I see that the two vectors that Orthogonalize generates are orthogonal in the standard dot-product sense for vectors, but I would think that for the cone of positive semidefinite matrices, you would want two matrices Y and Z such that
Trace[ Transpose[Y] . Z ] == 0.
It's not clear to me that the two matrices in proj satisfy that.
Thanks for the great blog! I'm learning a lot about convex optimization and Mathematica.
Adding identity matrix is simply there to center the region since I wanted the point 0,0 to be feasible. I should've said symmetric PSD matrices. For symmetric 4x4 matrices, there an orthonormal basis that can be indexed by coordinates x1,...,x10 and I'm finding orthonormal pair of vectors in that coordinate space. So the matrices are orthogonal if you take inner product corresponding to the space of symmetric matrices
ReplyDeleteThanks for the prompt and thorough response!
DeleteThese tips are really tremendous. Thank you for sharing with us. I think these tips are really effective for all in real estate dealing.
ReplyDeleteMathematica